ドットで線を描く

「2Dグラフィックスのしくみ」という本が面白かったです。メモリのデータはどのように画面に表示されるのかという話がわかりやすく書いてあります。2次元に並んだピクセル上に直線や円を表示したりベジェ曲線を描いたり、画像を加工したりペイントツールの仕組みの話があったり。

2Dグラフィックスのしくみ ――図解でよくわかる画像処理技術のセオリー WEB+DB PRESS plus

2Dグラフィックスのしくみ ――図解でよくわかる画像処理技術のセオリー WEB+DB PRESS plus

Amazon

この記事では直線を斜めに描くのと、ベジェ曲線を描くのをJavaScriptで実装してみました、という日記です。

See the Pen Dot Line by kariyayo (@kariyayo) on CodePen.

直線。

See the Pen Dot Bezier Curve by kariyayo (@kariyayo) on CodePen.

曲線。

直線を描く

Canvasにドットを打っていくことにします。

<body>
  <canvas id="canvas" width="400" height="400"></canvas>
</body>

const canvas = document.getElementById("canvas");
const context = canvas.getContext("2d");

まず、ドットを打つ関数を用意する。見やすいように1ドットの大きさを10ピクセル*10ピクセルとする。

/**
 * @param {int} x
 * @param {int} y
 * @param {object} color - {alpha: float, red: int, green: int, blue: int}
 */
function setDot(context, x, y, color) {
  context.fillStyle = `rgb(${color.red},${color.green},${color.blue})`;
  context.globalAlpha = color.alpha; // 透明度
  context.fillRect(x*10, y*10, 10, 10); // 10ピクセル*10ピクセルの大きさの矩形をドットとみなす
}

例として、 (0,0) ~ (4,3) の直線を引くことにする。直線を斜めに描くため2マスに跨ってしまうドットがある。具体的には (0,0) , (1, 3/4), (2, 6/3), (3, 9/4) , (4, 3) の5つのドットを打つことになる。これらのドットのうち、例えば (1, 3/4) は (1, 0) と (1,1) に跨ってしまう。

こういうドットは四捨五入してどっちかのマスに寄せることにする。

結果はこういう感じ。

https://i.gyazo.com/3310cfe5b0c0632f9106136e0f13177e.png

// (0,0) ~ (4,3) まで線を引く
const x1 = 0;
const y1 = 0;
const x2 = 4;
const y2 = 3;
const deltaY = (y2 - y1) / (x2 - x1); 
let y = y1
for (var x = 0; x < x2+1; x++) {
  const intY = Math.round(y);
  setDot(context, x, intY, {alpha:1.0, red:200, green:200, blue:200});
  y = y + deltaY;
}

しかし、x軸方向に1ずつ増やす処理にしているため (0,0) ~ (3,6) のように縦長だとうまくつながらない。

https://i.gyazo.com/7cd297ccdcc2aa5417630db0c77f6674.png

ちょっと改造するとうまくいく。

https://i.gyazo.com/9106dd02e4144061eccce1f13ab6c373.png

// (0,0) ~ (3,6) まで線を引く
const x1 = 0;
const y1 = 0;
const x2 = 3;
const y2 = 6;
const deltaY = (y2 - y1) / (x2 - x1);
let y = y1;
for (var x = 0; x < x2+1; x++) {
  const intY = Math.round(y);
  setDot(context, x, intY, {alpha:1, red:200, green:200, blue:200});

  // 縦が足りない部分のドット
  const nextY = Math.round(deltaY * (x + 1));
  for (var cy = intY+1; cy < nextY; cy++) {
    setDot(context, x, cy, {alpha:1, red:200, green:200, blue:200})
  }
  y = y + deltaY;
}

(5,5) ~ (40,15) のように、ちょっと長い直線を描くとガタガタになる。

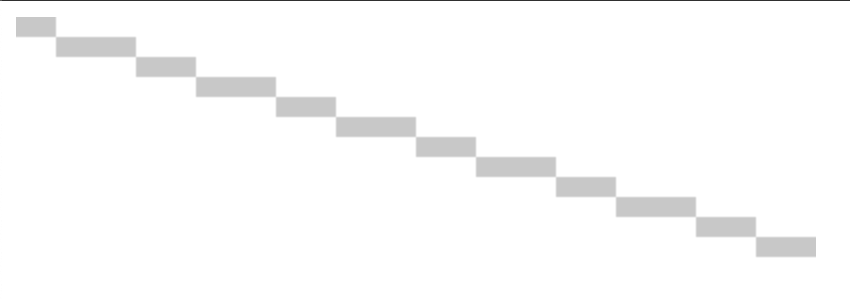
https://i.gyazo.com/776c65e1d679ba541b570536eff884be.png

そこで不透明度を使ってアンチエイリアシングする。

intY を求めるときに四捨五入（ Math.round() ）ではなく切り捨て（ Math.floor() ）して、差分 y - intY を f として求める。そして、 1 - f を不透明度とする。つまり差分が少ない=ドットが2つのマスに跨っていないほど、不透明度が1.0に近づくようにする。

https://i.gyazo.com/1ed375a4171daa5e4bc6bc776b03f1fe.png

// (5,5) ~ (40,15) まで線を引く
const x1 = 5;
const y1 = 5;
const x2 = 40;
const y2 = 15;
const deltaY = (y2 - y1) / (x2 - x1);
let y = y1;
for (var x = 0; x < x2+1; x++) {
  const intY = Math.floor(y);
  const f = y - intY;
  setDot(context, x, intY, {alpha:1-f, red:200, green:200, blue:200});
  setDot(context, x, intY+1, {alpha:f, red:200, green:200, blue:200})
  y = y + deltaY;
}

なかなか良い！

縦長だとまた繋がらなくなってしまったのでさっきと同じように改造すると良さそう。結果的にこうなった。

See the Pen Dot Line by kariyayo (@kariyayo) on CodePen.

曲線を描く

次は曲線。ベジェ曲線を描く。名前はよく聞くけど実際どうやって計算してるのかさっぱり知らなかった。

例えば、 (5,5) ~ (30, 12) の間に曲線を描きたい。途中に3点加えた計5点を制御点と呼ぶ。制御点とベジェ曲線の定義を使って曲線を描く。

https://i.gyazo.com/342ecfdcf9ac2926fb1eb33c8cdd8fe0.png

const ps = [
  {x: 5, y: 5},
  {x: 8, y: 18},
  {x: 20, y: 20},
  {x: 25, y: 3},
  {x: 30, y: 12},
];

setDot(context, ps[0].x, ps[0].y, {alpha:1.0, red:0, green:0, blue:200});
setDot(context, ps[1].x, ps[1].y, {alpha:1.0, red:200, green:200, blue:200});
setDot(context, ps[2].x, ps[2].y, {alpha:1.0, red:200, green:200, blue:200});
setDot(context, ps[3].x, ps[3].y, {alpha:1.0, red:200, green:200, blue:200});
setDot(context, ps[4].x, ps[4].y, {alpha:1.0, red:200, green:0, blue:0});

本には具体例の計算式が書いてる。一般化した定義はWikipediaを見てみる。ベジェ曲線 - Wikipedia

\displaystyle P(t) = \sum_{i=0}^{N-1}B_{i}J_{N-1,i}(t)
\displaystyle J_{n,i}(t) = \binom{n}{i}{}t^i (1-t)^{n-i}

x軸を1ずつ増やすたびに t を計算して P(t) を使って座標を求める。 J_{N-1,i}(t) はバーンスタイン基底関数と呼ばれる関数。

これらを実装する。

let combi = null;

/**
 * 組み合わせ（nCr）の計算
 */
function combination(n, r) {
  if (combi == null) {
    const pascalTriangl = (n) => {
      const pt = [];
      for (let i = 0; i < n+1; i++) {
        pt[i] = [];
        pt[i][0] = 1;
        pt[i][i] = 1;
        for (let j = 1; j < i; j++) {
          pt[i][j] = pt[i-1][j-1] + pt[i-1][j];
        }
      }
      return pt;
    }
    combi = pascalTriangl(n);
  }
  return combi[n][r];
}

/**
 * バーンスタイン基底関数
 */
function bernstein(n, i, t) {
  return combination(n, i) * (t**i) * ((1-t)**(n-i));
}

/**
 * P(t)
 */
function bezier(ps, t) {
  const n = ps.length;
  const p = ps.map((p, i) => {
      const b = bernstein(n-1, i, t);
      const px = p.x * b;
      const py = p.y * b;
      return {x: px, y: py};
    }).reduce((acc, v) => {
      return {x: acc.x + v.x, y: acc.y + v.y};
    }, {x: 0, y:0})
  }
  return p;
}

この bezier() （ベジェ曲線の定義）を使って曲線を描く。制御点毎に bezier() を使って座標を計算する。

const ps = [
  {x: 5, y: 5},
  {x: 8, y: 18},
  {x: 20, y: 20},
  {x: 25, y: 3},
  {x: 30, y: 12},
];

const start = ps[0];
const last = ps[ps.length-1];

for (var x = start.x; x <= last.x; x++) {
  const t = (x - start.x) / (last.x - start.x);
  let p = bezier(ps, t);
  p = {x: Math.floor(p.x), y: Math.floor(p.y)};
  setDot(context, p.x, p.y, {alpha:1.0, red:200, green:200, blue:200})
}
setDot(context, start.x, start.y, {alpha:1.0, red:0, green:0, blue:200}); // スタート地点は青
setDot(context, last.x, last.y, {alpha:1.0, red:200, green:0, blue:0}); // ゴール地点は赤

結果こんな感じ。線が途切れる。。

https://i.gyazo.com/3974797b2a82c26f1b97e4d921b5bf48.png

今のソースコードだとx軸方向に1ドット t を計算してベジェ曲線の定義で座標を求める。この座標を求める頻度を少し減らすことにする。始点から終点までを短い直線をつなげると考える。例えば、 (5,5) ~ (30,12) の区間を5分割して、5つの直線を繋ぎ合わせて曲線を表現する。そうすることで曲線が繋がるように調整できる。

先ほどの直線を描く処理を drawLine() 関数として定義する。

function drawLine(context, x1, y1, x2, y2, color) {
  const deltaY = (y2 - y1) / (x2 - x1);
  let y = y1;
  for (var x = x1; x < x2+1; x++) {
    const intY = Math.floor(y);
    const f = y - intY;
    setDot(context, x, intY, {alpha:1-f, red:color.red, green:color.green, blue:color.blue});
    setDot(context, x, intY+1, {alpha:f, red:color.red, green:color.green, blue:color.blue})

    y = y + deltaY;
  }
}

5分割してループする。ループ毎に分割された直線を描くためスタート地点とゴール地点の2つの座標を求める。 スタート地点用の t1 とゴール地点用の t2 を計算してそれぞれの座標を求め、drawLine() を使って直線を描く。

const ps = [
  {x: 5, y: 5},
  {x: 8, y: 18},
  {x: 20, y: 20},
  {x: 25, y: 3},
  {x: 30, y: 12},
];

const div = 5; //分割数
const deltaT = 1.0 / div;

for (var i = 0; i < div; i++) {
  const t1 = i / div;
  let p1 = bezier(ps, t1);
  p1 = {x: Math.floor(p1.x), y: Math.floor(p1.y)};

  const t2 = t1 + deltaT;
  let p2 = bezier(ps, t2);
  p2 = {x: Math.floor(p2.x), y: Math.floor(p2.y)};

  // 直線を描く
  drawLine(context, p1.x, p1.y, p2.x, p2.y, {alpha:1.0, red:200, green:200, blue:200})
}
setDot(context, ps[0].x, ps[0].y, {alpha:1.0, red:0, green:0, blue:200}); // スタート地点は青
setDot(context, ps[ps.length-1].x, ps[ps.length-1].y, {alpha:1.0, red:200, green:0, blue:0}); // ゴール地点は赤

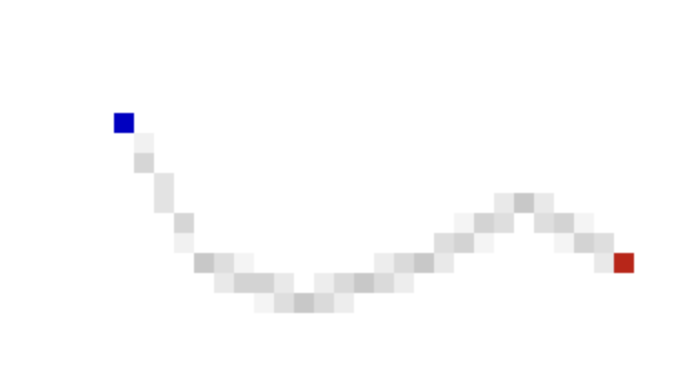
https://i.gyazo.com/d3ae2d410b9f3cb9706adee183758def.png

結果的にこうなった。曲線をどれくらい細かい直線に分割するか、というのが重要で、曲線の長さによって調整する必要があるらしい。

See the Pen Dot Bezier Curve by kariyayo (@kariyayo) on CodePen.

おしまい

面白い！けど本当に表層触っただけで沼がとても深そうだなと感じました！